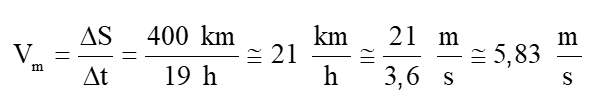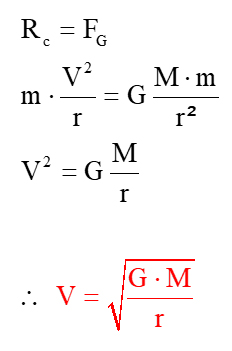A cápsula Space X Crew Dragon foi lançada ontem, 30 de maio, às 16h22 (horário de Brasília), em direção à ISS – Estação Espacial Internacional (ou Estação Espacial Internacional). Assista ao vídeo acima.
Ele foi para o espaço, alimentado por um moderno foguete SpaceX moderno Falcon 9, que carregava dois americanos – Robert Behnken e Douglas Hurle – para a missão oficial da NASA.
Enquanto escrevia este texto, no domingo (31) de manhã, a cápsula se aproximou da ISS, onde se juntou com sucesso por volta das 11h16 (horário brasileiro), para que os astronautas pudessem pousar a missão oficial em agosto. Eu acompanho o processo pelo canal do Youtube desde NASA TV e pela vida dos amigos da comunicação na ciência.
Vale lembrar que em 2011, após a aposentadoria da espaçonave, este foi o primeiro lançamento de um foguete na ISS que estava saindo do solo americano. Ele tem 9 anos! E este é o primeiro vôo de um piloto feito por uma empresa privada. Daí a dupla missão histórica!
A ISS orbita a Terra por cerca de 400 km, o que é praticamente a distância entre o Rio de Janeiro e São Paulo. Mas a viagem da cápsula para a estação espacial levou cerca de 19 horas, muito tempo para uma nave espacial tão rápida, certo?
Confira a imagem abaixo para obter uma expressão matemática da velocidade escalar média que aprendemos no ensino médio.
Se usarmos o conceito de velocidade escalar média (Vm), assumindo que o caminho da Terra para o ISS é ΔS = 400 km e dura dt = 19 h, podemos alcançar o valor real assumido da velocidade média de uma nave espacial nesta viagem espacial. Veja:
Atingimos um valor de 21 km / h ou, dividindo por 3,6, um fator de conversão de km / hum / s, 5,85 m / s Observe que o valor é compatível com a velocidade média de um reboque lento carregado com uma tonelada de carga que viaja entre duas capitais SP e RJ. Você pode viajar de bicicleta muito mais rápido que isso, concorda? Para uma nave espacial, esse não é um valor de velocidade muito baixo? Em outras palavras, por que um navio leva tanto tempo para chegar à ISS? Ou há algo errado com esta fatura / explicação? Meditar!
Antes de responder a essa pergunta, você sabe qual é a velocidade orbital da ISS? Ou, se você não se lembra do valor da cabeça, sabe como encontrá-lo? E Speed Crew Dragon, quanto vale? Vamos examinar essas idéias físicas curiosas primeiro.
Cálculo da velocidade orbital da ISS
Para simplificar, imagine que a ISS orbita a Terra em uma órbita perfeitamente circular e a uma altitude de h = 400 km. Aproximando o raio da Terra para R = 6400 km, a ISS executa uma órbita de raio r = R + h = 6800 km.
Força gravitacional FSENHOR que mantém essa órbita desempenha o papel da força centrípeta resultante¹, ou seja, puxa a ISS sempre em direção ao centro da Terra, impedindo que ela escape para o espaço pela tangente à órbita. Portanto, a força gravitacional FSENHOR cumpre o papel da força centrípeta resultante¹ RÇ.
A lei universal da gravidade nos diz o seguinte:
onde G = 6.67.10-11 N.m² / kg² é a constante de gravidade universal, M = 6.1024 kg é a massa da Terra, m é a massa da ISS er = R + h é a distância entre o centro da nave e o centro da Terra.
A segunda lei de Newton para a força centrípeta resultante¹ é dada:
onde m é a massa da ISS, V é sua velocidade orbital er = R + h é o raio de sua órbita ao redor da Terra para R é o raio da Terra e h é a altitude da ISS em relação à superfície da Terra (ou nível do mar).
Nós podemos concordar RÇ e FSENHOR, uma vez FSENHOR desempenha um papel RÇ no movimento orbital da ISS. E teremos:
Acima, mostramos que a velocidade orbital da ISS ou de qualquer satélite ao redor da Terra pode ser obtida:
Observe que na subtração a massa m da ISS é matematicamente cancelada, o que significa fisicamente que essa velocidade não depende da massa do corpo em órbita, mas apenas da massa M do corpo central, exceto a constante G e o raio r da órbita explicados na expressão acima.
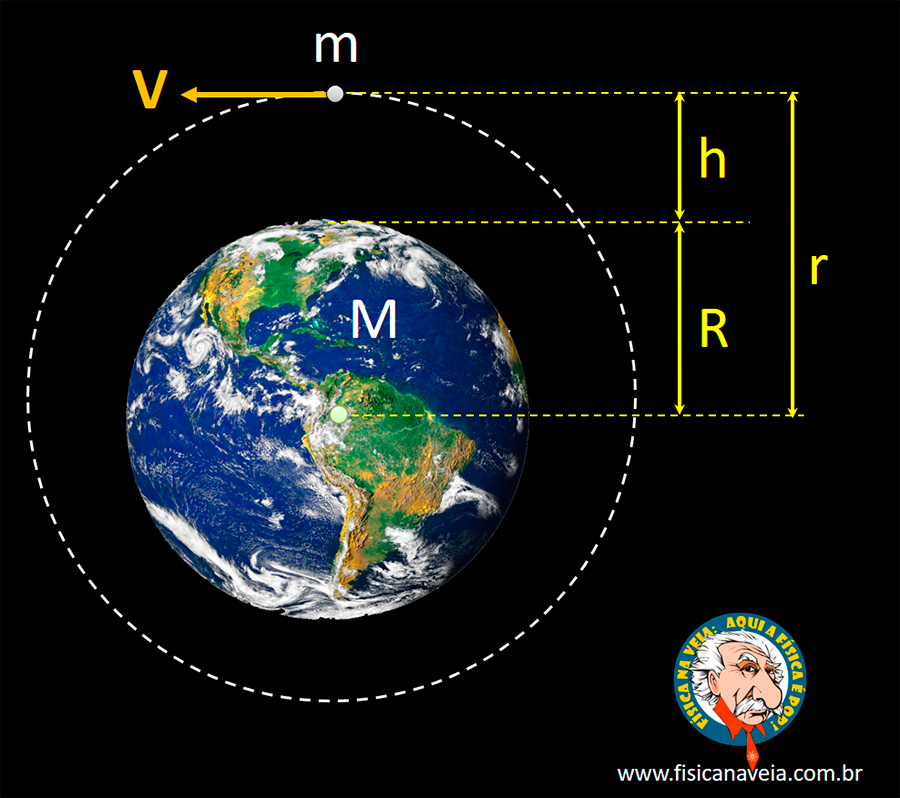
A idéia de uma ISS órbita aproximadamente circular de massa me raio r = R + h é mostrada na figura abaixo. Observe que a ilustração está intencionalmente fora de escala. E aqui está outro detalhe: a órbita da ISS não é perpendicular ao equador da Terra, como sugerido por uma ilustração que tem uma proposta didática apenas para exibir os parâmetros V, M, m, R, he er.
A partir da expressão acima, podemos finalmente calcular o valor da velocidade orbital do ISS², lembrando que seu raio orbital r mede nessas condições aproximadamente r = R + h = 6400 km + 400 km = 6,4.106 m + 0.4106 m = 6.8.106 m é a massa da Terra M = 6,1024 kg e o valor da constante gravitacional G = 6.7.10-11 N.m² / kg², todos os valores aproximados, mas dentro da precisão que precisamos para os propósitos deste texto. Verifique as contas abaixo:
Note que desta vez trabalhamos inicialmente no Sistema Internacional de Unidades e obtivemos uma velocidade orbital de um / s. Em seguida, multiplicamos por 3,6 para converter em km / h, a unidade mais familiar para nós, porque é usada nos velocímetros de nossos veículos aqui em Brasil.
De acordo com os cálculos acima, descobrimos que a ISS viaja pela Terra a uma velocidade orbital de cerca de 27.885 km / h em relação ao centro do nosso planeta, tomado como referência! Incrível, não é? Quase 30 vezes mais rápido que a velocidade de cruzeiro de um jato comercial! A essa velocidade, a ISS completa uma revolução na Terra a cada aproximadamente 1,5 horas!
No site www.isstracker.com você praticamente rastreia a ISS e em tempo real pode ver qual ponto da Terra está funcionando bem, sabendo sua altura e velocidade. Altere unidades (UNITS) para Metric para ver a altitude em km e a velocidade em m / s.
Crew Dragon está indo direto para a ISS, certo?
Não. Isso seria muito perigoso, porque a velocidade relativa entre a cápsula e a ISS seria muito alta! E esse é exatamente o “erro” na explicação e, portanto, no cálculo da velocidade média de aproximadamente 21 km / h para o navio lá no início do post! A viagem não é apenas 400 km. Eu explico a idéia melhor abaixo.
O que fazemos na prática de maneira simplificada é colocar uma cápsula com astronautas orbitando a Terra em uma órbita muito semelhante à da ISS, na mesma altitude h = 400 km. Portanto, a cápsula deve ter praticamente a mesma velocidade que a ISS, logo abaixo de 28.000 km / h, conforme calculado acima. De fato, a cápsula terá uma velocidade um pouco maior que a velocidade da ISS, o que significa que ela “perseguirá” a ISS em sua órbita e acessará a Estação Espacial de maneira segura e gradual para uma operação de atracação sensível.
Lembre-se de que a cápsula e a ISS viajarão pela Terra muito rapidamente. A velocidade que calculamos acima toma o centro da Terra como referência. Mas a velocidade relativa entre eles será pequena. Na prática, é como se a ISS estivesse em repouso e a cápsula chegasse a ela lentamente, controlada, manobrável e segura.
Para entender melhor a ideia, é como se tivéssemos dois carros descendo a estrada, um após o outro. A frente viaja a 108 km / h, ou 30 m / s, e a traseira 31 m / s.Este cenário, fisicamente, se tomarmos o carro da frente como referência, é como se estivesse parado, e a traseira viajou 31 – 30 = 1 m / si se aproximou. Em outras palavras, o veículo atrás dele está se aproximando lentamente do carro à frente a uma velocidade de 1 m por segundo, é muito pequeno, embora os dois estejam se movendo em alta velocidade em comparação com o asfalto.
É por isso que conectar a cápsula e a ISS leva 19 horas! A viagem não é apenas 400 km! Para que o Dragão Dragão alcance a altura orbital da ISS, 400 km acima da superfície do nosso planeta, em apenas 12 minutos. Imagine uma viagem do Rio de Janeiro a São Paulo em 12 minutos! Mas a jornada é muito maior do que apenas 400 km acima do nível do mar e corresponde a pouco mais de 12 círculos completos ao redor do nosso planeta para que o Dragão Dragão alcance gradualmente a ISS.
Você entendeu a ideia? E tudo é baseado na mecânica clássica bonita e muito bem-sucedida de Isaac Newton!
Que tal pilotar o Dragon Dragon e pousar na ISS?
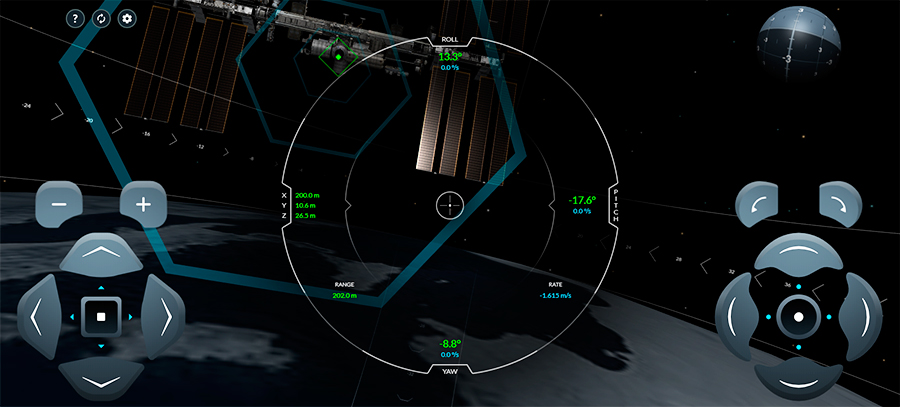
Para ter uma idéia das dificuldades de pilotar a tripulação do dragão e aterrissar na ISS, você pode usá-lo simulador no site do Space X. Nele, você controla os movimentos rotacionais (comandos à direita) e a tradução (comandos à esquerda) do Dragon Dragon “direcionando” o ponto de junção ISS do navio através da exibição principal no pára-brisa do navio. Tente! Você verá que não é fácil, porque no espaço todo comando para virar ou virar uma nave, devido à falta de resistência e inércia do ar, causa rotação infinita!
Boa festa!
Abraço do prof. Dulcidio! Física e astronáutica em uma veia!

Resultado A força centrípeta resultante é a força resultante que puxa o corpo em um movimento circular em direção ao centro da curva, impedindo que ele escape por inércia na direção tangencial;
² Esta expressão é muito mais geral e é usada para obter a velocidade orbital V de qualquer corpo m em torno de outro corpo M. Observe que, neste caso, apenas a massa M da velocidade orbital do corpo central é importante no cálculo do valor.
³ Inércia é a tendência que cada corpo deve seguir com o mesmo vetor de velocidade em que está localizado se a força resultante nele for igual a zero.
Para saber mais